Párhuzamos RC kör
Ismét kövessük a soros körök tárgyalásánál megszokott gyakorlatot, egyszerűsítsük az áramkört. Vizsgáljuk elsőként mélyebben a párhuzamos RC kört. Játszunk és számoljunk egy kicsit az alábbi animációs játékkal: Katt!
Magyarázat
Nézzük a tudományos magyarátatot!
A kapcsolás:
A vektorábrák:
Az ábrák alapján egyértelmű, hogy hogyan számítjuk (pitagorasz tétel alapján) az admittanciát:
Vizsgáljuk a frekvenciafüggést
Vizsgáljuk meg az előző képletet, ahonnan megállapíthatjuk, hogy kis frekvenciák esetén a kapacitív vezetés "kicsi", tehát az áramkör ohmos ellenállásként, míg nagy frekvenciákon pedig a kapacitív vezetés "nagy", mellette G elhanyagolható, így az áramkör kapacitásként fog viselkedni. (minden "megcserélődik a soros esethez képest).
A határfrekvenciát a kezdeti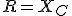 
feltételből vezetjük le:
Végül lássuk mindezt grafikusan is:
Kísérlet
Kísérlet:
Az elméleti ismereteink biztosabbá tételére álljon itt egy gyakorlati példa. Építsünk a TINA szoftware-el egy párhuzamos RC áramkört, és vizsgáljuk meg alacsony frekvencián és magas frekvencián, hogy mely ágban lesz domináns az áram! Mi a sejtésünk? Igazoljuk! Magyarázzuk meg!
A megépítendő áramkör:
